Union-Find
Reviewing what I studied, how this work will be explained as well.
Union-Find (Disjoint-Set) Concept
The Union-Find algorithm is used to manage disjoint-sets, which are collections of sets that are mutually exclusive, meaning they have no elements in common. This algorithm supports two primary operations: Find: This operation finds the representative element (root) of the set to which a given element belongs. Union: This operation merges two disjoint sets into one.
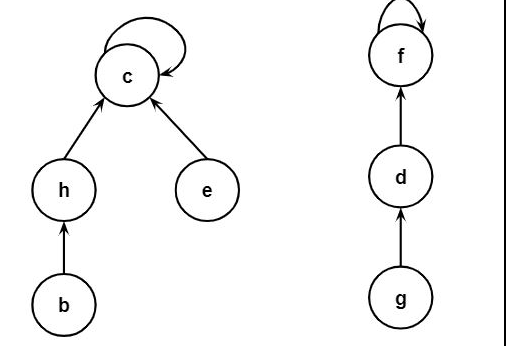
Disjoint-Set Tree
Disjoint-sets can be represented as a tree structure. Each node represents an element of a set, and child nodes point to their parents. The root node points to itself.
The Union-Find algorithm involves the following key operations:
- Make-Set: Initializes all elements to point to themselves.
- Find: Finds the root (representative element) of the set containing a given element.
- Union: Merges two disjoint sets into one.
int root[max_size];
// Similar to Make-Set function
for (int i = 0; i < max_size; i++) {
parent[i] = i;
}
int find(int x) { // O(1)
if (root[x] == x) {
return x;
}
else {
return find(root[x]);
}
}
void union(int x, int y) { // O(N)
x = find(x);
y = find(y);
root[y] = x; // set y's root to x's root
}
Optimization on Find / Union.
But there are two issues in the code above. If the depth of tree is 6, and to find that root node, we have to recursively go through 6 steps. Simply, why do we have to take 6 steps to find the root node? can we just make depth 1, but connected to all node! Yes! we can certainly! this method is called path compression.
Another issue would be union. Let’s assume I have trees A and B. A has depth (3), and B has depth (6), Then would it better to merge B into A or A into B? It’s better to merge tree that have lower depth to greater depth. For example, if we put A into B, then the depth of union tree doesn’t change, but if we union B to A, you will get +1 depth in resulting tree. So this can be managed by the concept of rank, which is similar to depth.
The below algorithm has path compression and union by rank applied.
struct UnionFind {
vector<int> parent; // parent link
vector<int> rank; // depth information
UnionFind(int n): parent(n), rank(n, 0) {
// set all element pointing to itself.
for(int i = 0; i < n; i++)
parent[i] = i; // make-set
}
int find(int x) {
if (parent[x] == x)
return x;
}
int merge(int x, int y) {
int x_set = find(x);
int y_set = find(y);
if (x_set == y_set)
return x_set
if (rank[x_set] < rank[y_set]){
return parent[xset] = yset;
} else {
if (rank[x_set] == rank[y_set])
rank[x_set]++
return parent[y_set] = x_set;
}
}
}
Time Complexity
Let’s look at the time complexity by the operation. makeSet is O(N) when n element is given. Find Operation is similar, but the worst case scenario it’s O(N). Since Union uses Find operation, it takes about O(N). Overall, it becomes O(N) times, but constant time O(a(n)) if path compression & union by rank. (a=> ackerman function).
