Introduction (Bottleneck of Ray Tracing Method)
Ray Tracing 으로 Rendering 을 하게 되면, 여러 Bottleneck 이 존재한다. 일단 모든 물체에 대해서 물체가 부딫혀서 색깔을 가져와야하며, 물체의 Material 이 Transparncy 나 Reflection 이 있다면 반사 또는 굴절(reflection ray & refracted ray) 를 만들어서 다시 쏴주는것도 한계가 있으며, 또 물체의 그림자를 표현하려면, shadow ray 를 만들어서 물체의 충돌을 계산해야한다. 그래서 실시간으로 Rendering 을 하기에는 Computation Expensive 하다. 물론, 다른 Data Structure 를 사용한다면, 분명 최적화가 가능하지만, 일단 이러한 점을 CPU 에서 해결하는게 효율적이지 못하다.
이걸 해결하기위한 방법이 Rasterization Algorithm 이다. 일단 Approach 자체가 다르다.
Rasterization Algorithm
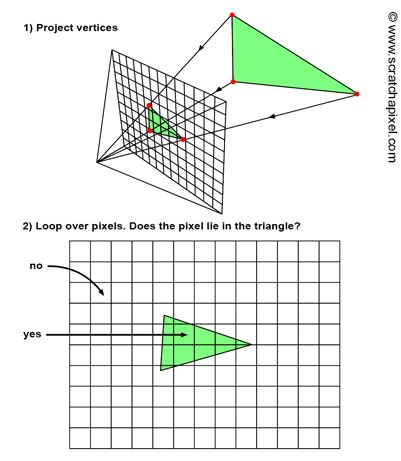
일단 앞서서, Ray Tracing 을 사용할때, 역방향으로 Ray 를 쏴줬다. 더 자세하게 설명을 하면, 우리가 보는 위치(눈) 에서 Ray 를 Screen 으로 100 개를쏴서, 그 100 개가 물체에 충돌하는지 충돌 안하는지를 계산을 했었다. 하지만, Rasterization 에서는 물체의 형상을 Screen 좌표계로 투영을 시킨다는 점이다. 즉 정점들을 Screen 좌표로 투영을 시켜서, 삼각형이라고 한다면, 그 3 개의 Vertex 를 정점을 투영시켜, 정점들을 연결시켜서 Render 또는 그리면 된다. 그래서 Screen 좌표 Block 에 삼각형이 들어있는지 없는지만 체크하면된다. 마치 충돌처럼 보일수는 있어도, Pixel 이 있는지 없는지만 확인을 하면 되기때문에, 더 빠르다. 아래의 그림을 보면 조금더 이해가 잘될거다.
Rasterization 의 알고리즘의 Step 은 Ray Tracing 과 비슷하면서도 다르다. 예를 들어서 Ray Tracing 같은 경우, 모든 Pixel 에 대해서 Loop 을 돌면서 모든 물체에 Hit 을 하는지 안하는지를 체크 한이후에, 물체에 부딫히면 물체의 색을 결정했었다. Rasterization 같은 경우, 기준이 scene 에있는 모든 물체에서 Loop 을 돌고, 그 이후에 모든 물체의 Vertex 들을 투영을 시킨다음에, 그다음에 Pixel 을 돌면서, 그 Pixel 이 물체안에 들어가있는지 없는지를 체크를 한이후에 들어가 있다면, color 값을 가지고 오면 된다. 여기서 중요한건 Rasterization Algorithm 은 object-centric 이라는 점이다. 즉 도형의 Geometry 를 image 좌표계로 바꿔서, 그 Image 를 Loop 을 돌기 때문이다.
즉, 가상공간에 있는 삼각형을 가지고, Screen 좌표계로 투영을 시킨 이후에, pixel 마다 체크 하면서, 삼각형 밖에 있는 Pixel 인가, 안에 있는 Pixel 인가 체크 하면서, 들어있을때는 Screen 에다가 색깔을 칠해주고, 아니면 색깔을 안칠하면 되는 식이다. 근데 모든 Pixel 을 돌게 되면 되게 비효율적이다. 그래서 가장 작은 Bounding Box 를 그려서 효율성을 높인다.
Rasterization Prep
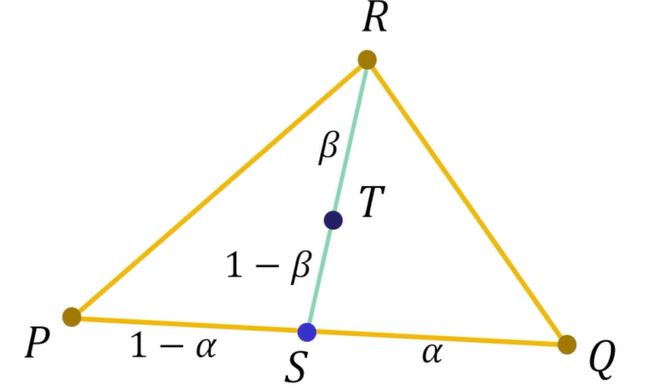
- Baycentric Coordinates 여기에서 알아볼 점은, 삼각형 정점
PQR이 존재한다고 했을때 그 안에 T 를 Affine Sum 으로 표현하는게 중요하다.
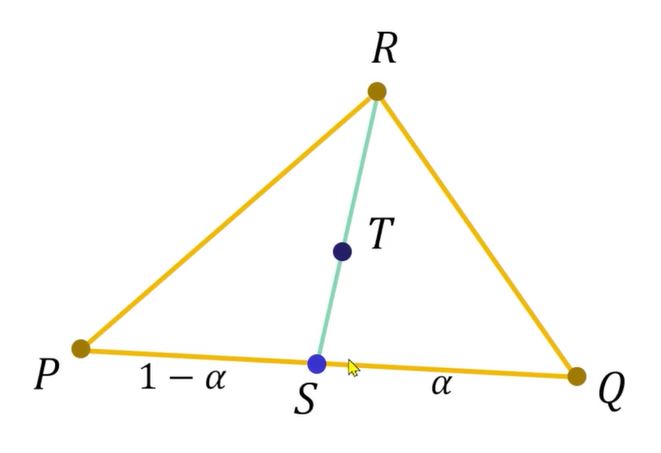
위의 그림과 같이 R 의 좌표와 T 의 좌표를 이미 알기때문에, R 과 T 를 포함하는 직선을 그려서, PQ 직선의 점 S 에 그리게 되면 P 와 S 의 거리, S 와 Q 의 거리의 비를 찾을수 있다. 그러면 S 의 위치를 S = P + (1 - alpha)(Q - P) 라는 식을 구할수있다.
그 이후에, 아래와 같이 T 의 위치를 PQ 에서 S 의 위치를 구하듯이, Beta 를 이용해서 구할수 있다. 그래서 T = beta * S + (1 - beta)*R 이런식으로 구한다음에 S 의 값을 위의 식에 대입을 하면 T 의 좌표를 Affine Combination 을 구할수 있다. T = alpha * beta * P + beta(1 - alpha)*Q + (1 - beta)*R 이런식으로 표현이 된다.
Rasterization Implementation (How to draw Triangle)
언제나 삼각형 그리는게 기본중에 기본이다. 일단 Rasterization 어떻게 구현해야될지 class 구조를 짜보자. 일단 Header 파일에서 Rasterization 의 생성자를 만들때, with 와 height 의 정보를 가지고 오며, ProjectWorldToRaster 같은 경우는 World 좌표계에 정의된 정점들을 Screen 좌표계로 이동시키면 되는 함수가 있으며, Util Function 으로는 Edge Function 이 있다. 그리고 Render 와 매 Frame 마다 Update 를 하는 Update 함수가 있다.
using namespace glm;
using namespace std;
struct Vertex
{
vec3 pos;
vec3 color;
};
struct Triangle
{
Vertex v0, v1, v2;
};
class Rasterization
{
public:
Rasterization(const int &width, const int &height)
vec2 ProjectWorldToRaster(vec3 point);
float EdgeFunction(const vec2 &v0, const vec2 &v1, const vec3 &point);
void Render(vector<vec4> &pixels);
void Update();
public:
int width;
int height;
Triangle triangle;
};
void Rasterization::Rasterization(const int &width, const int &height)
: width(width), height(height)
{
triangle.v0.pos = {0.0, 0.5, 1.0f};
triangle.v1.pos = {1.0, -0.5, 1.0f};
triangle.v2.pos = {-1.0, -0.5, 1.0f};
triangle.v0.color = {1.0f, 0.0f, 0.0f}; // Red
triangle.v1.color = {0.0f, 1.0f, 0.0f}; // Green
triangle.v2.color = {0.0f, 0.0f, 1.0f}; // Blue
}
void Rasterization::Render(vector<vec4> &pixels)
{
// Compute World Coordinates to Screen Coordinates
const auto v0 = ProjectWorldToRaster(triangle.v0.pos);
const auto v1 = ProjectWorldToRaster(triangle.v1.pos);
const auto v2 = ProjectWorldToRaster(triangle.v2.pos);
// Find the bounding box
const auto xMin = size_t(glm::clamp(glm::floor(std::min({v0.x, v1.x, v2.x})), 0.0f, float(width - 1)));
const auto yMin = size_t(glm::clamp(glm::floor(std::min({v0.y, v1.y, v2.y})), 0.0f, float(height - 1)));
const auto xMax = size_t(glm::clamp(glm::ceil(std::max({v0.x, v1.x, v2.x})), 0.0f, float(width - 1)));
const auto yMax = size_t(glm::clamp(glm::ceil(std::max({v0.y, v1.y, v2.y})), 0.0f, float(height - 1)));
for(size_t j = yMin; j<= yMax; j++){
for(size_t i = xMin; i <= xMax; i++){
// Check if the pixel is inside of triangle
// Get the pixel info
// A Parallel Algorithm for Polygon Rasterization
const vec2 point = vec2(float(i), float(j));
const float alpha0 = EdgeFunction(v1, v2, point);
const float alpha1 = EdgeFunction(v2, v0, point);
const float alpha2 = EdgeFunction(v0, v1, point);
if (alpha0 >= 0.0f && alpha1 >= 0.0f && alpha2 >= 0.0f) {
const float area = alpha0 + alpha1 + alpha2;
const float w0 = alpha0 / area;
const float w1 = alpha1 / area;
const float w2 = alpha2 / area;
const vec3 color = (w0 * triangle.v0.color + w1 * triangle.v1.color + w2 * triangle.v2.color);
pixels[i + width * j] = vec4(color, 1.0f);
}
}
}
}
vec2 Rasterization::ProjectWorldToRaster(vec3 point)
{
// ** Orthographics Projection ** //
// Convert to NDC(Normalized Device Coordinates)
// NDC Range [-1, 1] x [-1, 1]
const float aspect = float(width) / height;
const vec2 pointNDC = vec2(point.x / aspect, point.y)
// Rasterization Coordinates Range: [-0.5, width -1 + 0.5] x [-0.5, height - 1 + 0.5]
const float xScale = 2.0f / width;
const float yScale = 2.0f / height;
// NDC -> Rasterization
return vec2((pointNDC.x + 1.0f) / xScale - 0.5f, (1.0f - pointNDC.y) / yScale - 0.5f);
}
float Rasterization::EdgeFunction(const vec2 &v0, const vec2 &v1, const vec2 &point)
{
const vec2 a = v1 - v0;
const vec2 b = point - v0;
return (a.x * b.y - a.y * b.x) * 0.5;
}
여기서 중요한건 위와 같이 Render 를 할때, 각 정점을 Orthographics Projection 해주는 함수 ProjectWorldToRaster 를 통해서, Screen 좌표계로 옮겨주고, Bounding Box 를 찾을수 있게 해준다음에, Bounding Box 안에서 Edge Function 알 사용해서, Pixel 이 삼각형 안에 들어가져있는지 없는지 확인을 한 이후에, Barycentric Coordinates 을 사용해서 Pixel 값을 정해주면 된다. 참고: Edge Function 같은 경우, Pixel 이 삼각형안에 들어왔는지 없는지를 확인 하는 함수이다. 아래의 그림을 참고하자.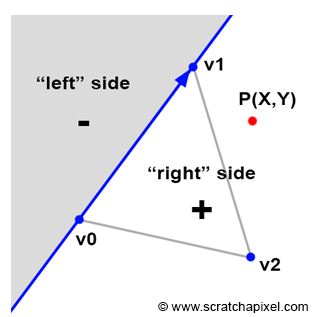
그래서 삼각형의 결과는 이러하다.