DirectX11 - Fresnel & Schlick Approximation

in Study on DirectX, Computer Graphics, Hlsl

“Fresnel Reflection describe the behavior of light when moving between media of differing refractive indices”. 결국 말을 하는건 빛이 다른 굴절률(Refractive Index) 가지고 있는 물질(Media) 에 어떻게 표현하는지를 나타낸다고 한다. 아래의 그림처럼, 다른 n1, n2 물질이 있다고 하면, 빛은 일부는 반사하고, 일부는 굴절한다. 그걸 표현한게 아래의 그림이다. 그리고 Snell’s law 를 통하면, 각 Incident Angle 과 Refractive Angle 의 관계를 표현을 하면 sin(theta(i)) / sin(theta(t)) = n2/n1 표현을 할수 있다.

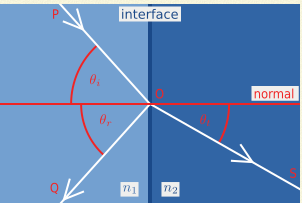
alt text

그렇다면, 이 식을 어떻게 이제껏 사용했던걸로 사용하자면, Specular(반사광) 에다가 곱해주면 된다. 일단 물질의 고유의 값을 표현할 NameSpace 로 묶어 준다. 그리고 결국엔 이 값들을 Material 값들을 ConstantBuffer 안에다가 같이 넣어주면 된다.

namespace FresnelConstant {
constexpr Vector3 Water(0.02f, 0.02f, 0.02f);
constexpr Vector3 Glass(0.08, 0.08, 0.08);
constexpr Vector3 Plastic(0.05, 0.05, 0.05);
constexpr Vector3 Silver(0.95, 0.93, 0.88);
constexpr Vector3 Copper(0.95, 0.64, 0.54);
}; // namespace FresnelConstant

struct Material {
    Vector3 ambient = Vector3(0.0f);  // 12
    float shininess = 0.01f;           // 4
    Vector3 diffuse = Vector3(0.0f);  // 12
    float dummy1;                     // 4
    Vector3 specular = Vector3(1.0f); // 12
    float dummy2;                     // 4
    Vector3 fresnelR0 = FresnelConstant::Water; // 12
    float dummy3;
};

그이후에 CPU 에서 어떻게 Resource 가 Binding 되는건 생략을 하도록 하자.

HLSL 쪽을 한번 보자. SchlicFresnel 의 공식은 아래와 같다.

alt text

그리고 HLSL 에서 표현을 하면, 아래와 같이 표현이 가능하다. 여기에서 1 - cosTheta 가 결국에는 내가 바라보는 각도에따라서 Normal 과 90 도라고 한다면, 0 이 되므로, 가장자리쪽이고, 0 에 가까우면 가장자리가 아니라는것이다, 즉 가장자리라고 함은 빛을 더많이 받고, 그렇지 않는 경우에는 값이 작은 값들이 들어오고, Cubemap 에 있는걸 그대로 빛출것이다.

float3 SchlickFresnel(float3 fresnelR0, float3 normal, float3 toEye)
{
    float cosTheta = saturate(dot(normal, toEye));
    return fresnelR0 + (1.0 - fresnelR0) * pow(1 - cosTheta, 5.0);
}

결과는 아래와 같다. 아래의 그림처럼, 가장자리 쪽에는 굉장히 많은 빛을 받아서, Specular 값이 쎄고, 안쪽은 빛을 덜받기에 약간의 Diffuse 를 얻는것을 확인 할 수 있다.

alt text

Resource